a) Chứng minh rằng OH < OK.. Câu 10 trang 101 Sách Bài Tập (SBT) Toán 9 Tập 2 - Bài 2: Liên hệ giữa cung và dây
Cho tam giác ABC có AB > AC. Trên cạnh AB lấy một điểm D sao cho hạ AD = AC.
Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường thẳng vuông góc OH, OK xuống BC và BD (\(H \in BC,K \in BD\)).
a) Chứng minh rằng OH < OK.
b) So sánh hai cung nhỏ BD và BC.
Giải
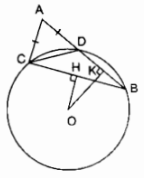
a) Trong ∆ABC ta có:
BC > AB – AC (bất đẳng thức tam giác)
Advertisements (Quảng cáo)
Mà AC = AD (gt)
\( \Rightarrow \) BC > AB – AD
Hay BC > BD
Trong (O) ta có: BC > BD
\( \Rightarrow \) OH < OK (dây lớn hơn gần tâm hơn)
b) Ta có dây cung BC > BD
Suy ra: \(\overparen{BC}\) > \(\overparen{BD}\) (dây lớn hơn căng cung lớn hơn).
