a) Hai cung nhỏ CF và DB bằng nhau.
. Câu 12 trang 101 Sách Bài Tập (SBT) Toán 9 Tập 2 – Bài 2: Liên hệ giữa cung và dây
Advertisements (Quảng cáo)
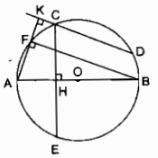
Cho đường tròn tâm O. Trên nửa đường tròn bán kính AB lấy hai điểm C, D.
Từ C kẻ vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E.
Từ A kẻ vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F.
Chứng minh rằng:
a) Hai cung nhỏ CF và DB bằng nhau.
b) Hai cung nhỏ BF và DE bằng nhau
c) DE = BF.
Giải
a) ∆ AFB nội tiếp trong (O) có
AB là đường kính nên ∆ AFB vuông tại F.
\( \Rightarrow BF \bot AK\)
Advertisements (Quảng cáo)
\(AK \bot CD\) (gt)
Suy ra: BF // CD
\( \Rightarrow \) \(\overparen{BD}\) = \(\overparen{CF}\) (hai cung chắn giữa hai dây song song thì bằng nhau)
b) \(AB \bot CE\) tại điểm H nên C và H đối xứng qua trục AB.
\( \Rightarrow \) \(\overparen{BC}\) = \(\overparen{BE}\)
\(\overparen{CF}\) = \(\overparen{BD}\) (chứng minh trên)
Suy ra: \(\overparen{BC}\) + \(\overparen{CF}\) = \(\overparen{BE}\) + \(\overparen{BD}\)
Hay \(\overparen{BF}\) = \(\overparen{DE}\)
c) \(\overparen{BF}\) = \(\overparen{DE}\) (chứng minh trên)
d) BF = DE(hai cung bằng nhau căng hai dây bằng nhau).