Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn.. Câu 13 trang 101 Sách Bài Tập (SBT) Toán 9 Tập 2 - Bài 2: Liên hệ giữa cung và dây
Cho đường tròn (O). Gọi I là điểm chính giữa dây cung AB (Không phải là cung nửa đường tròn) và H là trung điểm của dây AB. Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn.
Giải
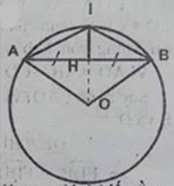
Ta có: \(\overparen{IA}\) = \(\overparen{IB}\)(gt)
\( \Rightarrow IA = IB\) (2 cung bằng nhau căng 2 dây bằng nhau)
\( \Rightarrow I\) nằm trên đường trung trực của AB
Advertisements (Quảng cáo)
OA = OB (bán kính (O)
\( \Rightarrow O\) nằm trên đường trung trực của AB
Suy ra: OI là đường trung trực của AB
H là trung điểm của AB, do đó OI đi qua trung điểm H
Vậy 3 điểm I, H, O thẳng hàng.
