Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.. Câu 18 trang 159 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 2. Đường kính và dây của đường tròn
Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
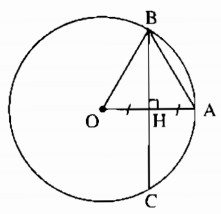
Gọi I là trung điểm của AB
Suy ra: \(IO = IA = {1 \over 2}OA = {3 \over 2}\)
Ta có: BC ⊥OA (gt)
Suy ra: \(\widehat {OIB} = 90^\circ \)
Advertisements (Quảng cáo)
Áp dụng định lí Pi-ta-go vào tam giác vuông OIB ta có: \(O{B^2} = B{I^2} + I{O^2}\)
suy ra: \(B{I^2} = O{B^2} - I{O^2}\)
\(={3^2} - {\left( {{3 \over 2}} \right)^2} = 9 - {9 \over 4} = {{27} \over 4}\)
\(BI ={{3\sqrt 3 } \over 2}\) (cm)
Ta có: BI = CI (đường kính dây cung)
Suy ra: \(BC = 2BI=2.{{3\sqrt 3 } \over 2} = 3\sqrt 3 \) (cm)