a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN.
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho
AM = BN. Qua M và qua N, kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.

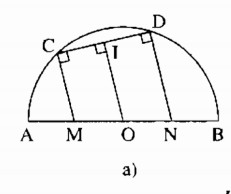
a) Ta có: CM ⊥CD
DN⊥CD
Suy ra: CM // DN
Kẻ OI ⊥CD
Suy ra: OI // CM // DN
Ta có: IC = ID (đường kính dây cung)
Suy ra: OM = ON (1)
Mà: AM + OM = ON + BM( = R) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: AM = BN.
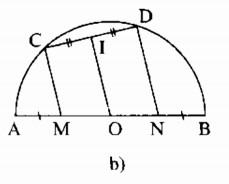
b) Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.
