Câu 19 trang 167 Sách Bài Tập (SBT) Toán 9 Tập 2:Tính diện tích toàn phần S....

Cho hình bình hành ABCD với AB = 1, AD = x (x > 0) và \(\widehat {BAD} = 60^\circ \).

a) Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S₁ của hình tạo thành khi quay quanh cạnh AD.

b) Xác định giá trị x khi S = S₁ và S = 2S₁.

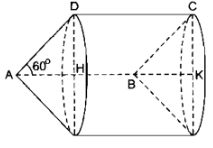
a) khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên 2 hình nón bằng nhau có đường sinh AD = BC = x,  cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình tròn.

Trong ∆AHD có \(\widehat {AHD} = 90^\circ ;\widehat A = 60^\circ \)

        DH = AD. sin60º = \(x.{{\sqrt 3 } \over 2} = {{x\sqrt 3 } \over 2}\)

Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh 2 hình nón và diện tích xung quanh hình trụ: S = S­_{xq trụ} + 2S_{xq nón}

\(\eqalign{
& S = 2\pi DH.DC + 2.\pi DH.AD \cr
& = 2\pi {{x\sqrt 3 } \over 2}.1 + 2.\pi .{{x\sqrt 3 } \over 2}.x \cr
& = \pi x\sqrt 3 + \pi {x^2}\sqrt 3 \cr} \)

\( \Rightarrow S = \pi x\sqrt 3 (1 + x)\)

Khi quay hình bình hành quanh trục AD một vòng thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = CD = 1. Cạnh AD vạch nên hình trụ có bán kính đáy bằng bán kính nón.

Bán kính đáy: DH = AB. sin60º = \({{\sqrt 3 } \over 2}.\)

S₁: diện tích toàn phàn hình tạo thành bằng tổng diện tích xung quanh hai hình nón cộng với diện tích hình trụ.

         S₁ = S_{xq trụ}  + 2.S_{xq nón}

\({S_1} = 2.\pi .DH.AD + 2.\pi .DH.AB = 2\pi {{\sqrt 3 } \over 2}.x + 2.\pi .{{\sqrt 3 } \over 2}.1\)

\({S_1} = \pi \sqrt 3 (x + 1)\)

b) Để S = S₁ \(\Rightarrow \pi x\sqrt 3 (1 + x) = \pi \sqrt 3 (x + 1) \Leftrightarrow x(1 + x) = x + 1\)

\( \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow (x + 1)(x - 1) = 0\)

Vì x > 0 \( \Rightarrow \) x + 1 # 0 \( \Rightarrow \) x – 1 = 0 \( \Leftrightarrow \) x = 1

Để S =2S₁ \(\Rightarrow \) \(\pi x\sqrt 3 (1 + x) = 2\pi \sqrt 3 (x + 1) \Leftrightarrow x(x + 1) = 2(x + 1)\)

\( \Leftrightarrow \) x² – x – 2 = 0 \( \Leftrightarrow \) x² – 2x  + x – 2 = 0 \( \Leftrightarrow \) (x – 2)(x + 1) = 0

Vì x > 0 \( \Rightarrow \) x + 1 # 0 \( \Rightarrow \) x – 2 = 0 \( \Leftrightarrow \) x = 2