Câu 2.1 trang 101 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho đường tròn tâm O bán kính R. Vẽ góc ở tâm \(\widehat {AOB} = {80^0}\), vẽ góc ở tâm \(\widehat {BOC} = {120^0}\) kề với \(\widehat {AOB}\).
So sánh và sắp xếp độ dài AB, BC, CA theo thứ tự tăng dần.
Giải

Ta có: \(\widehat {AOB} = {80^0}\); \(\widehat {BOC} = {120^0}\)
Suy ra: \(\widehat {AOC} = {160^0}\)
sđ \(\overparen{AB}\) \( = \widehat {AOB}\)
sđ \(\overparen{BC}\) \( = \widehat {BOC}\)
sđ \(\overparen{AC}\) \( = \widehat {AOC}\)
\(\widehat {AOB} < \widehat {BOC} < \widehat {AOC}\)
Suy ra \(\overparen{AB}\) < \(\overparen{BC}\) < \(\overparen{AC}\)
Suy ra: AB < BC < AC
Câu 2.2 trang 101 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho hình thoi ABCD. Vẽ đường tròn tâm A, bán kính AD. Vẽ đường tròn tâm C, bán kính CB. Lấy điểm E bất kỳ trên đường tròn tâm A (không trùng với B và D), điểm F trên đường tròn tâm C sao cho BF song song với DE.
So sánh hai cung nhỏ DE và BF.
Advertisements (Quảng cáo)
Giải
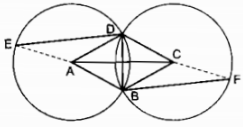
Ta có (A; AD) và (C; CB) có bán kính AD = CB là cạnh của hình thoi ABCD nên hai đường tròn đó bằng nhau.
Vì AD = AB = CD = CB
Suy ra (A; AD) và (C; CB) cắt nhau tại B và D.
DE // BF (gt)
\( \Rightarrow \widehat {EDB} = \widehat {FBD} \Rightarrow \widehat {EDA} + \widehat {ADB} = \widehat {FBC} + \widehat {CBD}\)
\(\widehat {ADB} = \widehat {CBD}\) (tính chất hình thoi)
Suy ra: \(\widehat {EDA} = \widehat {FBC}\) (1)
∆ADE cân tại A \( \Rightarrow \widehat {EAD} = {180^0} - 2\widehat {EDA}\) (2)
∆CBF cân tại C \( \Rightarrow \widehat {BCF} = {180^0} - 2\widehat {FBC}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {EAD} = \widehat {BCF}\)
sđ \(\overparen{DE}\) \( = \widehat {EAD}\)
sđ \(\overparen{BF}\) \( = \widehat {BCF}\)
Vì (A; AD) và (C; CB) bằng nhau nên \(\overparen{DE}\) = \(\overparen{BF}\)
