Cho tam giác ABC có cạnh BC cố định và \(\widehat A = \alpha \) không đổi. Tìm quỹ tích giao điểm của ba đường phân giác trong của tam giác đó.
Giải
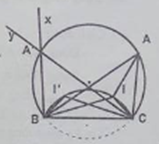
Chứng minh thuận: Gọi I là giao điểm 3 đường phân giác trong của ∆ABC
\(\widehat {IBC} = {{\widehat B} \over 2};\widehat {ICB} = {{\widehat C} \over 2}\)
\( \Rightarrow \) \(\widehat {IBC} + \widehat {ICB} = {{\widehat B + \widehat C} \over 2}\) mà trong ∆ABC ta có: \(\widehat B + \widehat C = 180^\circ - \widehat A = 180^\circ - \alpha \)
Suy ra: \(\widehat {IBC} + \widehat {ICB} = {{180^\circ - \alpha } \over 2}\)
Trong ∆BIC ta có: \(\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\)
Suy ra: \(\widehat {BIC} = 180^\circ - {{180^\circ - \alpha } \over 2} = {{360^\circ - 180^\circ + \alpha } \over 2} = 90^\circ + {\alpha \over 2}\)
Α không đổi \( \Rightarrow \widehat {BIC} = 90^\circ + {\alpha \over 2}\) không đổi.
I thay đổi tạo với 2 đầu đoạn BC cố định một góc bằng 90º + \({\alpha \over 2}\) không đổi
Advertisements (Quảng cáo)
Vậy I nằm trên cung chứa góc 90º + \({\alpha \over 2}\) vẽ trên BC.
Chứng minh đảo: Trên cung chứa góc 90º + \({\alpha \over 2}\) lấy điểm I’ bất kỳ. Vẽ trên cùng nửa mặt phẳng bờ BC chứa điểm I’ hai tai Bx và Cy sao cho BI’ là phân giác của \(\widehat {CBx},CI’\) là phân giác của \(\widehat {BCy}\).
Bx cắt Cy tại A¢.
Trong ∆BI¢C ta có: \(\widehat {BI’C} = 90 + {\alpha \over 2}\)
\( \Rightarrow \widehat {I’BC} + \widehat {I’CB} = 180^\circ - \widehat {BI’C} = 180^\circ - \left( {90^\circ + {\alpha \over 2}} \right) = {{180^\circ - \alpha } \over 2}\)
\(\widehat {CBA’} = 2\widehat {I’BC};\widehat {BCA’} = 2\widehat {I’CB}\)
\( \Rightarrow \widehat {CBA’} + \widehat {BCA’} = 2.{{180^\circ - \alpha } \over 2} = 180^\circ - \alpha \)
Trong ∆A¢BC ta có:
\(\widehat {BA’C} = 180^\circ - (\widehat {CBA’} + \widehat {BCA’}) = 180^\circ - (180^\circ - \alpha ) = \alpha \)
Vậy quỹ tích giao điểm 3 đường phân giác trong ∆ABC khi \(\widehat A = \alpha \) không đổi, BC cố định là 2 cung chứa góc \(90^\circ + {\alpha \over 2}\) vẽ trên BC..
