Cho tam giác nhọn MNP. Câu 4.8 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đó kẻ từ M. Chứng minh rằng:
a) \({S_{MNP}} = {1 \over 2}MP.NP.\sin P\);
b) \(DP = {{MN.\sin N} \over {tgP}}\);
c) ∆DNE đồng dạng với ∆MNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P.
Gợi ý làm bài
Advertisements (Quảng cáo)
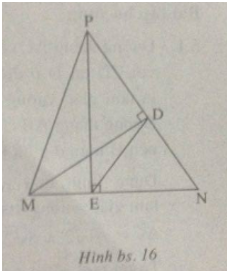
(h.bs. 16)
a) Ta có MD = MP sin P, suy ra:
\({S_{MNP}} = {1 \over 2}NP.MD = {1 \over 2}NP.MP\sin P.\)
b) Ta có MD = MN sin N và MD = DP tg P nên từ đó suy ra DP \( = {{MN\sin N} \over {tgP}}\)
c) Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên \({{DN} \over {MN}} = {{EN} \over {PN}}.\)
Hai tam giác DNE và MNP đồng dạng vì có góc N chung và \({{DN} \over {MN}} = {{EN} \over {PN}}.\)