Chứng minh BSCE là một tứ giác nội tiếp.. Câu 40 trang 106 Sách Bài Tập (SBT) Toán 9 Tập 2 - Bài 7: Tứ giác nội tiếp
Cho tam giác ABC. Các đường phân giác trong của \(\widehat B\) và \(\widehat C\) cắt nhau tại S, các đường phân giác ngoài của \(\widehat B\) và \(\widehat C\) cắt nhau tại E. Chứng minh BSCE là một tứ giác nội tiếp.
Giải
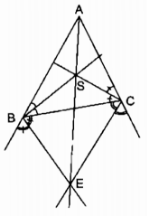
BS ⊥ BE (tính chất hai góc kề bù)
\( \Rightarrow \widehat {SBE} = 90^\circ \)
Advertisements (Quảng cáo)
CS ⊥ CE (tính chất hai góc kề bù)
\( \Rightarrow \widehat {SCE} = 90^\circ \)
Xét tứ giác BSCE ta có: \(\widehat {SBE} + \widehat {SCE} = 180^\circ \)
Vậy tứ giác BSCE nội tiếp.
