Trên đường tròn tâm O có một cung AB và S là điểm chính giữa của cung đó.
Trên dây AB lấy hai điểm E và H. Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D. Chứng minh EHCD là một tứ giác nội tiếp.
Giải
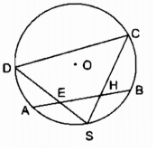
S là điểm chính giữa của cung \(\overparen{AB}\).
\( \Rightarrow \) \(\overparen{SA}\) = \(\overparen{SB}\) (1)
Advertisements (Quảng cáo)
\(\widehat {DEB} = {1 \over 2}\) (sđ \(\overparen{DCB}\) + sđ \(\overparen{AS}\)) tính chất góc có đỉnh ở bên trong đường tròn) (2)
\(\widehat {DCS} = {1 \over 2}\) sđ \(\overparen{DAS}\) (tính chất góc nội tiếp) hay \(\widehat {DCS} = {1 \over 2}\) (sđ \(\overparen{DA}\) + sđ \(\overparen{SA}\)) (3)
Từ (1) và (2) suy ra: \(\widehat {DEB} + \widehat {DCS} = {1 \over 2}\) (sđ \(\overparen{DCB}\) + sđ \(\overparen{AS}\) + sđ \(\overparen{DA}\) + sđ \(\overparen{SA}\) (4)
Từ (1) và (4) suy ra: \(\widehat {DEB} + \widehat {DCS} = {1 \over 2}\) (sđ \(\overparen{DCB}\) + sđ \(\overparen{BS}\) + sđ \(\overparen{SA}\) + sđ \(\overparen{DA}\) \( = {{360^\circ } \over 2} = 180^\circ \)
Hay \(\widehat {DEH} + \widehat {DCH} = 180^\circ \)
Vậy: tứ giác EHCD nội tiếp được trong một đường tròn.
