Trả lời câu hỏi Bài 7 trang 88 Toán 9 Tập 2. Vậy \(\widehat {BAD} + \widehat {BCD} = 180^\circ \) .. Bài 7. Tứ giác nội tiếp
Xem hình 45. Hãy chứng minh định lý trên.
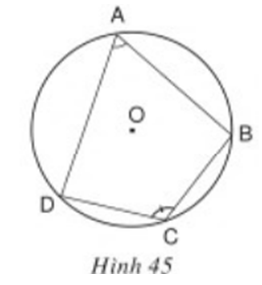
Sử dụng:
Số đo góc nội tiếp bằng nửa số đo cung bị chắn.
Số đo cả đường tròn bằng \(360^0.\)
Advertisements (Quảng cáo)
Xét đường tròn \((O)\) ta có:
\(\widehat {BAD} = \dfrac{1}{2}sđ\,\overparen {BCD}\) (góc nội tiếp chắn cung \(BCD\))
\(\widehat {BCD} = \dfrac{1}{2}sđ\,\overparen {BAD}\) (góc nội tiếp chắn cung \(BAD\))
Suy ra \(\widehat {BAD} + \widehat {BCD} = \dfrac{1}{2}sđ\,\overparen {BCD} + \dfrac{1}{2}sđ\,\overparen {BAD} = \dfrac{{sđ\,\overparen {BAD} + sđ\,\overparen {BCD}}}{2}\) \( = \dfrac{{360^\circ }}{2} = 180^\circ .\)
Vậy \(\widehat {BAD} + \widehat {BCD} = 180^\circ \) .
Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \(180^0\).