Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA.
a) Tứ giác OCAD là hình gì ? Vì sao?
b) Kẻ tiếp tuyến đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R.

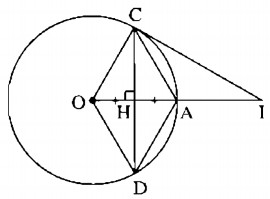
a) Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Advertisements (Quảng cáo)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Đồng thời CD ⊥ OA nên ACOD là hình thoi.
b) Vì ACOD là hình thoi nên AC = OC
Mà OC = OA ( = R) nên tam giác OAC đều
Suy ra: \(\widehat {COA} = 60^\circ \) hay \(\widehat {COI} = 60^\circ \)
Mà CI ⊥ OC (tính chất tiếp tuyến)
Trong tam giác vuông OCI, ta có:
\(CI = OC.tg\widehat {COI} = R.tg60^\circ = R\sqrt 3 \).
