Cho tam giác cân ABC có đáy BC và \(\widehat A = {20^0}\). Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và \(\widehat {DAB} = {40^0}\). Gọi E là giao điểm của AB và CD.
a) Chứng minh ABCD là tứ giác nội tiếp
b) Tính \(\widehat {AED}\)
Giải
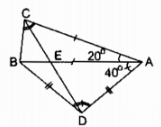
a) ∆ABC cân tại A (gt).
\( \Rightarrow \widehat {ACB} = \widehat {ABC}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {ACB} = {{180^\circ - \widehat A} \over 2} = {{180^\circ - 20^\circ } \over 2} = 80^\circ \)
∆DAB cân tại D.
\( \Rightarrow \widehat {DBA} = \widehat {DAB}\) (tính chất tam giác cân) mà \(\widehat {DAB} = 40^\circ \) (gt) \( \Rightarrow \widehat {DBA} = 40^\circ \)
Advertisements (Quảng cáo)
\(\widehat {ADB} = 180^\circ - (\widehat {DAB} + \widehat {DBA}) = 180^\circ - (40^\circ + 40^\circ ) = 100^\circ \)
Trong tứ giác ACBD ta có: \(\widehat {ACB} + \widehat {ADB} = 80^\circ + 100^\circ = 180^\circ \)
Vậy: Tứ giác ACBD nội tiếp.
b) Tứ giác ACBD nội tiếp
\(\widehat {BAC} = {1 \over 2}\) sđ \(\overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{BC}\)\( = 2\widehat {BAC} = 2.20^\circ = 40^\circ \)
\(\widehat {DBA} = {1 \over 2}\) sđ \(\overparen{AD}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AD}\) \( = 2\widehat {DBA} = 2.40^\circ = 80^\circ \)
\(\widehat {AED}\) là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác ACBD
\(\widehat {AED} = {1 \over 2}\)(sđ \(\overparen{BC}\) + sđ \(\overparen{AD}\)) \( = {{40^\circ + 80^\circ } \over 2} = 60^\circ \)
