Cho hình:
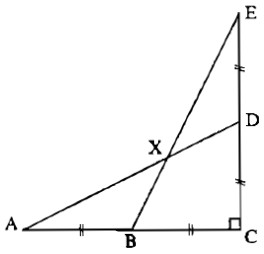
Biết:
\(\widehat {ACE} = 90^\circ ,AB = BC = CD = DE = 2cm.\)
Hãy tính:
a) AD, BE;
b) \(\widehat {DAC}\);
c) \(\widehat {BXD}\).

a) Ta có:
\(AC = AB + BC = 2 + 2 = 4\left( {cm} \right)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD, ta có:
Advertisements (Quảng cáo)
\(A{D^2} = A{C^2} + C{D^2} = {4^2} + {2^2} = 16 + 4 = 20\)
\( \Rightarrow AD = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
Mặt khác: \(CE = CD + DE = 2 + 2 = 4\left( {cm} \right)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông BEC, ta có:
\(B{E^2} = B{C^2} + C{E^2} = {2^2} + {4^2} = 4 + 16 = 20\)
\( \Rightarrow BE = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
b) Tam giác ACD vuông tại C nên ta có: \(tg\widehat {DAC} = {{CD} \over {AC}} = {2 \over 4} = {1 \over 2}\)
Suy ra: \(\widehat {DAC} \approx 26^\circ 34’\)
Ta có: \(\widehat {CDA} = 90^\circ - \widehat {CAD} \approx 90^\circ - 26^\circ 34′ = 63^\circ 26’\)
Trong tứ giác BCDX, ta có:
\(\widehat {BXD} = 360^\circ - (\widehat C + \widehat {CDA} + \widehat {CBE})\)
\( = 360^\circ - (90^\circ + 63^\circ 26′ + 63^\circ 26′) = 143^\circ 8′.\)
