Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M,N là các tiếp điểm).
a) Chứng minh rằngOA ⊥ MN.
b) Vẽ đường kính NOC. Chứng minh rằng MC // AO.
c) Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm.

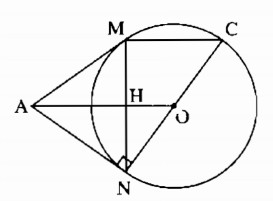
a) Ta có: AM = AN ( tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN ( tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
b) Tam giác MNC nội tiếp trong đường tròn (O)
có NC là đường kính nên \(\widehat {CMN} = 90^\circ \)
suy ra: MN ⊥ MC
Advertisements (Quảng cáo)
Mà OA ⊥ MN (chứng minh trên)
Suy ra: OA // MC
c) Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pi-ta-go vào tam giác vuông AON ta có:
\(A{O^2} = A{N^2} + O{N^2}\)
Suy ra: \(A{N^2} = A{O^2} - O{N^2} = {5^2} - {3^2} = 16\)
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: \(MH = NH = {{MN} \over 2}\) (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
\(OA.NH = AN.ON \Rightarrow NH = {{AN.ON} \over {AO}} = {{4.3} \over 5} = 2,4 (cm) \)
MN = 2.NH = 2.2,4 = 4,8 (cm).
