Câu 53 trang 109 SBT Toán 9 Tập 2: Tính độ dài đường tròn ngoại tiếp....

Tính độ dài đường tròn ngoại tiếp:

a) Một lục giác đều có cạnh là 4cm;

b) Một hình vuông có cạnh là 4cm;

c) Một tam giác đều có cạnh là 6cm.

Giải

a) Cạnh lục giác đều nội tiếp trong đường tròn (O; R) bằng bán kính R. Vì cạnh lục giác đều là 4cm \( \Rightarrow R = 4\) cm.

C = 2πR = 2. π. 4 = 8π (cm)

b) Đường tròn ngoại tiếp hình vuông có đường kính là đường chéo của hình vuông.

Độ dài đường chéo hình vuông có cạnh bằng 4 (cm) là \(4\sqrt 2 \) (cm)

Bán kính của đường tròn ngoại tiếp hình vuông:

\(R = {{4\sqrt 2 } \over 2} = 2\sqrt 2 \)

C = 2πR= 2. π. \(2\sqrt 2 \) = 4π\(\sqrt 2 \) (cm)

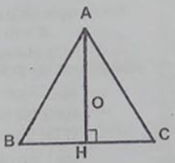
c) Vì tam giác đều nên giao điểm 3 đường trung trực cũng là giao điểm 3 đường cao, 3 đường trung tuyến nên bán kính của đường tròn ngoại tiếp bằng \({2 \over 3}\) đường cao của tam giác đều.

\(AH = AB.\sin \widehat B = {\rm{6}}.\sin {\rm{6}}{0^0} = {\rm{6}}.{{\sqrt 3 } \over 2} = 3\sqrt 3 \)

\(R = {2 \over 3}AH = {2 \over 3}.3\sqrt 3  = 2\sqrt 3 \) (cm)

C = 2πR = 2π.  = 4π  (cm).