Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I; r).

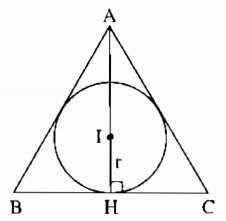
Gọi H là tiếp điểm của đường tròn (I) với BC.
Ta có: IH ⊥ BC (tính chất tiếp tuyến)
Vì I là tâm đường tròn nội tiếp tam giác ABC nên AI là tia phân giác của góc BAC.
Tam giác ABC đều nên AI cũng là đường cao của tam giác ABC. Khi đó A, I, H thẳng hàng.
Ta có: HB = HC ( tính chất tam giác đều)
Advertisements (Quảng cáo)
Tam giác ABC đều nên I cũng là trọng tâm của tam giác ABC.
Suy ra: AH = 3.HI = 3.r
\(\widehat {HAB} = {1 \over 2}\widehat {BAC} = {1 \over 2}.60^\circ = 30^\circ \)
Tam giác ABH vuông tại H nên ta có:
\(BH = AH.tg\widehat {HAB} = 3{\rm{r}}.tg{30^0} = 3{\rm{r}}.{{\sqrt 3 } \over 3} = r\sqrt 3 \)
Mà: \(BC = 2.BH = 2r\sqrt 3 \)
Vậy \({S_{ABC}} = {1 \over 2}AH.BC = {1 \over 2}.3r.2r\sqrt 3 = 3{r^2}\sqrt 3 \) (đvdt)
