Chứng minh rằng nếu tam giác ABC có chu vi 2p,bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức. Câu 57 trang 165 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 6. Tính chất của hai tiếp tuyến cắt nhau
Chứng minh rằng nếu tam giác ABC có chu vi 2p,bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức:
S = p.r

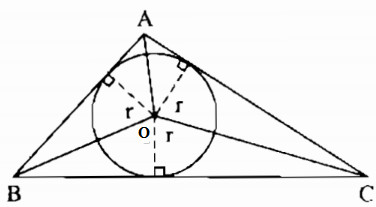
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC.
Advertisements (Quảng cáo)
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBC.
Ta có: \({S_{ABC}} = {S_{OAB}} + {S_{OAC}} + {S_{OBC}}\)
\(= {1 \over 2}.AB.r + {1 \over 2}.AC.r + {1 \over 2}.BC.r\)
\(= {1 \over 2}(AB + AC + BC).r\)
Mà AB + AC + BC = 2p
Nên \({S_{ABC}} = {1 \over 2}.2p.r = p.r\)
