Cho đường tròn (O; 3cm) và điểm A có AO = 5cm. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Tính độ dài OH.
b) Qua điểm M bất kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE.

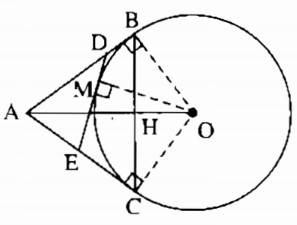
a) Ta có: AB = AC (tính chất hai tiếp tuyến cắt nhau).
Suy ra ∆ABC cân tại A.
AO là tia phân giác của góc BAC (tính chất
hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác ABC (tính chất
tam giác cân).
Ta có: AO vuông góc với BC tại H
Lại có: AB ⊥ OB (tính chất tiếp tuyến)
Tam giác ABO vuông tại B có BH ⊥ AO
Advertisements (Quảng cáo)
Theo hệ thức lượng trong tam giác vuông, ta có:
\(O{B^2} = OH.OA \Rightarrow OH = {{O{B^2}} \over {OA}} = {{{3^2}} \over 5} = 1,8\) (cm)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABO, ta có:
\(A{O^2} = A{B^2} + B{O^2}\)
Suy ra: \(A{B^2} = A{O^2} - B{O^2} = {5^2} - {3^2} = 16\)
AB = 4 (cm)
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB
= 2.4 = 8 (cm).
