Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn vuông góc với nhau tại A (B và C là các tiếp điểm).
a) Tứ giác ABOC là hình gì? Vì sao?
b) Gọi M là điểm bất kì thuộc cung nhỏ BC. Qua M kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE.
c) Tính số đo góc DOE.

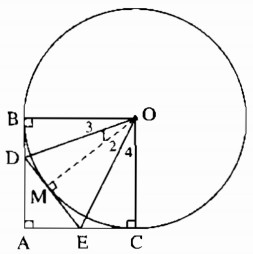
a) Ta có: \(AB ⊥ AC \Rightarrow \widehat {BAC} = 90^\circ \)
\(AB ⊥ BO \Rightarrow \widehat {ABO} = 90^\circ \)
\( AC ⊥ CO \Rightarrow \widehat {ACO} = 90^\circ \)
Tứ giác ABOC có 3 góc vuông nên nó là hình chữ nhật.
Mặt khác: AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra tứ giác ABOC là hình vuông.
b) Theo tính chất hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
Advertisements (Quảng cáo)
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC
= AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)
c) Theo tính chất hai tiếp tuyến cắt nhau ta có:
OD là tia phân giác của góc BOM
Suy ra: \(\widehat {BOD} = \widehat {DOM} = {1 \over 2}\widehat {DOM}\)
OE là tia phân giác của góc COM
Suy ra: \(\widehat {COE} = \widehat {EOM} = {1 \over 2}\widehat {COM}\)
Suy ra:
\(\widehat {DOE} = \widehat {DOM} + \widehat {EOM} \)
\(= {1 \over 2}(\widehat {BOM} + \widehat {COM})\)
\(= {1 \over 2}\widehat {COB} = {1 \over 2}90^\circ = 45^\circ \).
