Cho tam giác cân ABC có \(\widehat B = {120^0}\), AC = 6cm. Tính độ dài đường tròn ngoại tiếp tam giác đó.
Giải
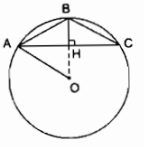
∆ABC cân có \(\widehat B\) = 1200 nên ∆ABC cân tại B
\( \Rightarrow \widehat A = \widehat C = {{{{180}^0} - {{120}^0}} \over 2} = {30^0}\)
Kẻ \(BH \bot AC \Rightarrow AH = HC = {1 \over 2}AC = 3\) (cm)
Trong tam giác vuông BHA ta có \(\widehat {BHA} = {90^0}\)
\(AB = {{AH} \over {\cos A}} = {3 \over {\cos {{30}^0}}} = {3 \over {{{\sqrt 3 } \over 2}}} = 2\sqrt 3 \) (cm)
Advertisements (Quảng cáo)
\(\widehat C = {1 \over 2}\widehat {AOB}\) (hệ quả góc nội tiếp)
\( \Rightarrow \widehat {AOB} = 2\widehat C = {2.30^0} = {60^0}\)
OA = OB (bán kính)
Suy ra ∆AOB đều nên OA = OB = \(2\sqrt 3 \) (cm)
Độ dài đường tròn ngoại tiếp ∆ABC
C = \(2\pi R\)
\(C = 2\pi .2\sqrt 3 = 4\pi \sqrt 3 \) (cm)
