Cho tam giác ABC, đường tròn (K) bằng tiếp góc trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng:
a) \(AE = AF = {{a + b + c} \over 2}\)
b) \(BE = {{a + b - c} \over 2};\)
c) \(CF = {{a + c - b} \over 2}\)

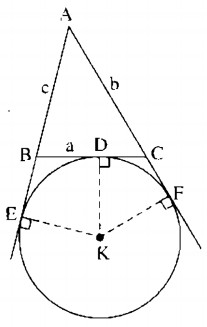
a) Gọi D là tiếp điểm của đường tròn (K) với cạnh BC.
Theo tính chất hai tiếp tuyến cắt nhau ta có:
BE = BD; CD = CF
Advertisements (Quảng cáo)
AE = AB + BE
AF = AC + CF
Suy ra: AE + AF = AB + BE + AC + CF
= AB + AC + (BD + DC)
= AB + AC + BC = c + b + a
Mà AE = AF (tính chất hai tiếp tuyến cắt nhau)
Suy ra: \({\rm{AE = AF = }}{{a + b + c} \over 2}\)
b) Ta có: \(BE = AE – AB = {{a + b + c} \over 2} - c = {{a + b - c} \over 2}\)
c) Ta có: \(CF = AF – AC = {{a + b + c} \over 2} - b = {{a + c - b} \over 2}.\)
