Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua một điểm M thuộc nửa hình tròn, kẻ tiếp tuyến thứ ba cắt Ax, By theo thứ tự ở C, D. Gọi N là giao điểm của AD và BC, H là giao điểm của MN và AB. Chứng minh rằng:
a) MN ⊥ AB;
b) MN = NH.

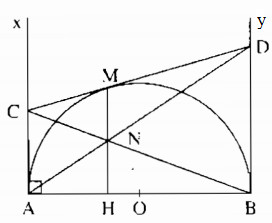
a) Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có: AC // BD
Suy ra: \({{ND} \over {NA}} = {{BD} \over {AC}}\) (Hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: \({{ND} \over {NA}} = {{MD} \over {MC}}\)
Trong tam giác ACD, ta có: \({{ND} \over {NA}} = {{MD} \over {MC}}\)
Suy ra: MN // AC ( Theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB
b) Trong tam giác ACD, ta có: MN // AC
Suy ra: \({{MN} \over {AC}} = {{DN} \over {DA}}\) (Hệ quả định lí Ta-lét) (3)
Trong tam giác ABC, ta có: MH // AC ( vì M, N, H thẳng hàng)
Suy ra: \({{HN} \over {AC}} = {{BN} \over {BC}}\) (Hệ quả định lí Ta-lét) (4)
Trong tam giác BDN, ta có: AC // BD
Suy ra: \({{ND} \over {NA}} = {{BN} \over {NC}}\) (Hệ quả định lí Ta-lét)
\( \Rightarrow {{ND} \over {DN + NA}} = {{BN} \over {BN + NC}} \Leftrightarrow {{ND} \over {DA}} = {{BN} \over {BC}}\) (5)
Từ (3), (4) và (5) suy ra: \({{MN} \over {AC}} = {{HN} \over {AC}} \Rightarrow MN = HN\).
