Cho tam giác ABC vuông cân có AB = AC = 12cm. Điểm M chạy trên AB) Tứ giác MNCP là một hình bình hành có đỉnh N thuộc cạnh AC (h.6). Hỏi khi M cách A bao nhiêu thì diện tích của hình bình hành bằng 32cm2?
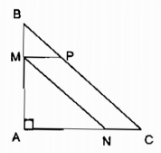

Gọi độ dài đoạn MA = x cm; điều kiện 0 < x < 12
Vì ∆ ABC vuông cân tại A nên tam giác BMP vuông cân tại M
⇒ MP = MB = AB – AM = 12 – x (cm)
Advertisements (Quảng cáo)
Diện tích hình bình hành MNCP bằng MP.MA
Suy ra: MP.MA = (12 – x)x
Ta có phương trình:
\(\eqalign{
& \left( {12 - x} \right)x = 32 \cr
& \Rightarrow {x^2} - 12x + 32 = 0 \cr
& \Delta ‘ = {\left( { - 6} \right)^2} - 1.32 = 36 - 32 = 4 > 0 \cr
& \sqrt {\Delta ‘} = \sqrt 4 = 2 \cr
& {x_1} = {{6 + 2} \over 1} = 8 \cr
& {x_2} = {{6 - 2} \over 1} = 4 \cr} \)
Cả hai giá trị x1 = 8 và x2 = 4 thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A là 8cm hoặc 4cm
