Tính diện tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng . Câu 64 trang 115 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
Tính diên tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 100\(^\circ \).
Gợi ý làm bài
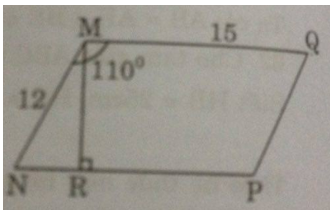
Giả sử hình bình hành MNPQ có MN = 12cm, MQ = 15cm, \(\widehat {NMQ} = 110^\circ \)
Ta có: \(\widehat {NMQ} + \widehat {MNP} = 180^\circ \) (hai góc trong cùng phía)
Suy ra: \(\widehat {MNP} = 180^\circ - \widehat {NMQ}\)
Advertisements (Quảng cáo)
\( = 180^\circ - 110^\circ = 70^\circ \)
Kẻ \(MR \bot NP\)
Trong tam giác vuông MNR, ta có:
\(\eqalign{
& MR = MN.\sin \widehat {MNP} \cr
& = 12.\sin 70^\circ \approx 11,276\,(cm) \cr} \)
Vậy \({S_{MNPQ}} = MN.NP \approx 11,276.15 = 169,14\) (cm2).