Hai ròng rọc có tâm O, O’ và bán kính R = 4a, R’ = a. Hai tiếp tuyến chung MN và PQ cắt nhau tại A theo góc 600. Tìm độ dài của dây cua- roa mắc qua hai dòng dọc.
Giải
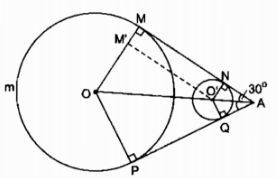
Vì hai tiếp tuyến chung của đường tròn (O) và (O’) cắt nhau tại A nên O, O’, A thẳng hàng.
\(\widehat {OAM} = \widehat {OAP} = {1 \over 2}\widehat {MAP}\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {OAM} = {30^0}\)
Trong tam giác vuông OMA có \(\widehat {OMA} = {90^0}\)
\( \Rightarrow MA = OM.\cot \widehat {OAM}\)
\( = 4a\cos {30^0} = 4a\sqrt 3 \)
Trong tam giác vuông O’NA có\(\widehat {O’NA} = {90^0}\)
\( \Rightarrow NA = O’N\cot \widehat {O’AN} = a\cot {30^0} = a\sqrt 3 \)
Advertisements (Quảng cáo)
\(MN = MA - NA = 4a\sqrt 3 - a\sqrt 3 = 3a\sqrt 3 \)
Trong tứ giác O’NAQ có \(\widehat N = \widehat Q = {90^0}\); \(\widehat A = {60^0}\)
Suy ra: \(\widehat {NO’Q} = {120^0}\)
Độ dài cung nhỏ \(\overparen{NQ}\) là: \({l_1} = {{\pi .a.120} \over {180}} = {{2\pi a} \over 3}\)
Trong tứ giác OMAP có \(\widehat M = \widehat P = {90^0}\); \(\widehat A = {60^0}\\)
Suy ra: \(\widehat {MOP} = {120^0}\) nên số đo cung nhỏ \(\overparen{MP}\) bằng 1200
sđ \(\overparen{MnP}\) \( = {360^0} - {120^0} = {240^0}\)
Độ dài cung lớn \(\overparen{MnP}\) là \({l_2}\) \( = {{\pi .4a.240} \over {180}} = {{16\pi a} \over 3}\)
Chiều dài của dây cua – roa mắc qua hai ròng rọc là:
\(2MN + {l_1} + {l_2} = 2.3a\sqrt 3 + {{2\pi a} \over 3} + {{16\pi a} \over 3}\(
=\(6a\sqrt 3 + 6\pi a = 6a\left( {\sqrt 3 + \pi } \right)\)
