Cho tam giác ABC vuông ở A và đường cao AH. Vẽ đường tròn tâm O đường kính AB. Biết BH = 2cm và HC = 6cm. Tính:
a) Diện tích hình tròn (O).
b) Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ).
c) Diện tích hình quạt tròn AOH (ứng với cung nhỏ AH).
Giải
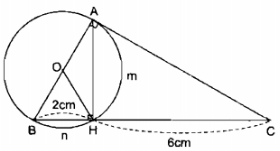
a) ∆ABC có \(\widehat A = {90^0}\)
Theo hệ thức lượng trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Rightarrow A{B^2} = 2.\left( {2 + 6} \right) = 16\)
AB = 4 (cm)
Diện tích hình tròn tâm O là:
\(S = \pi {\left( {{{AB} \over 2}} \right)^2} = \pi {\left( {{4 \over 2}} \right)^2} = 4\pi \) (cm2)
b) Tổng diện tích hai hình viên phân AmH
Advertisements (Quảng cáo)
Và BnH bằng diện tích nửa hình tròn tâm O trừ diện tích ∆AHB
Trong tam giác vuông ABC ta có:
\(A{H^2} = HB.HC = 2.6 = 12\)
AH = \(2\sqrt 3 \) (cm)
SAHB = \({1 \over 2}AH.BH = {1 \over 2}.2.2\sqrt 3 = 2\sqrt 3 \) (cm2)
Tổng diện tích hai hình viên phân là:
\(S = 2\pi - 2\sqrt 3 = 2\left( {\pi - \sqrt 3 } \right)\) (cm2)
c) ∆BOH có OB = OH = BH = 2 cm
\( \Rightarrow \Delta BOH\) đều
\( \Rightarrow \widehat B = {60^0}\)
\(\widehat B = {1 \over 2}\) sđ \(\overparen{AmH}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AmH}\) \( = 2\widehat B = {120^0}\)
Squạt AOH = \({{\pi {{.2}^2}.120} \over {360}} = {{4\pi } \over 3}\) (cm2)
