Cho đường tròn (O ; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A ; 2R).. Câu 79 trang 170 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
Cho đường tròn (O ; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A ; 2R).
a) Hai đường tròn (O) và (A) có vị trí tương đối như thế nào đối với nhau?
b) Gọi B là một giao điểm của hai đường tròn trên. Vẽ đường kính BOC của đường tròn (O). Gọi D là giao điểm ( khác C) của AC và đường tròn (O). Chứng minh rằng AD = DC.
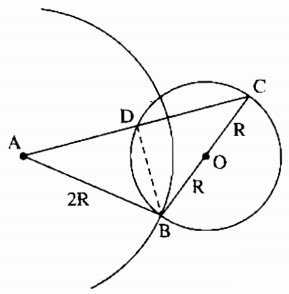
a) Ta có: R < OA < 3R ⇔ 2R- R < OA < 2R + R
Advertisements (Quảng cáo)
Suy ra hai đường tròn (O; R) và (A; 2R) cắt nhau.
b) Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên \(\widehat {BDC} = 90^\circ \)
Suy ra: BD ⊥ AC (1)
Ta có: AB = 2R và BC = 2OB = 2R
Suy ra tam giác ABC cân tại B (2)
Từ (1) và (2) suy ra: AD = DC