Trong một tam giác với các cạnh có độ dài 6,7,9, kẻ đường cao đến cạnh lớn nhất. Hãy tìm độ dài đường cao này và các đoạn thẳng mà nó định ra trên cạnh lớn nhất đó.
Gợi ý làm bài
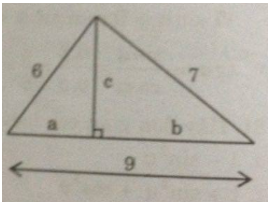
Gọi độ dài đường cao là c, hình chiếu cả hai cạnh 6 và 7 trên cạnh có độ dài bằng 9 lần lượt là a và b.
Ta có: a < b (6 < 7)
Theo định lí Pi-ta-go, ta có:
\({c^2} = {6^2} - a\)
\({c^2} = {7^2} - {b^2}\)
Suy ra: \(36 - {a^2} = 49 - {b^2}\)
Advertisements (Quảng cáo)
\( \Leftrightarrow {b^2} - {a^2} = 49 - 36\)
\( \Leftrightarrow (b + a)(b - a) = 13\,(*)\)
Mà x +y = 9 nên:
\(\eqalign{
& 9.(b - a) = 13 \Leftrightarrow b - a = {{13} \over 9} \cr
& \Rightarrow b = a + {{13} \over 9} \cr} \)
Thay vào (*), ta có:
\(\left[ {\left( {a + {{13} \over 9}} \right) + a} \right].{{13} \over 9} = 13 \Leftrightarrow 2a + {{13} \over 9} = {{13} \over {{{13} \over 9}}}\)
\(\eqalign{
& \Leftrightarrow 2a + {{13} \over 9} = 13.{9 \over {13}} \Leftrightarrow 2a + {{13} \over 9} = 9 \cr
& \Leftrightarrow a = {{9 - {{13} \over 9}} \over 2} = {{34} \over 9} \cr} \)
Suy ra: \(b = 9 - a = 9 - {{34} \over 9} = {{47} \over 9}\)
\(c = \sqrt {49 - {{\left( {{{47} \over 9}} \right)}^2}} \approx 4,7\)
