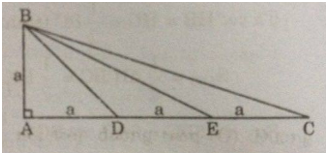
Tam giác ABC vuông tại A, AB = a, AC = 3a. trên cạnh AC lấy các điểm D, E sao cho
AD = DE = EC.
a) Chứng minh: \({{DE} \over {DB}} = {{DB} \over {DC}}\)
b) Chứng minh ∆BDE đồng dạng ∆CDB
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách
Cách 1: sử dụng kết quả ở câu b);
Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.
Gợi ý làm bài
a) Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
\(B{D^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2}\)
Suy ra: \(BD = a\sqrt 2 \)
Ta có:
\(\eqalign{
& {{DE} \over {DB}} = {a \over {a\sqrt 2 }} = {{\sqrt 2 } \over 2}; \cr
& {{DB} \over {DC}} = {{a\sqrt 2 } \over {2a}} = {{\sqrt 2 } \over 2} \cr} \)
Vậy \({{DE} \over {DB}} = {{DB} \over {DC}}\)
b) Xét ∆BDE và ∆CDB, ta có:
\({{DE} \over {DB}} = {{DB} \over {DC}}\,(1)\)
\(\widehat {BDE} = \widehat {BDC}\,(2)\)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra ∆BDE đồng dạng ∆CDB.
c) * Cách 1:
Ta có: ∆BDE đồng dạng ∆CDE \(\Rightarrow \widehat {BED} = \widehat {CBD}\)
Mặt khác:
\(\widehat {AEB} + \widehat {BCD} = \widehat {BED} + \widehat {BCD} = \widehat {CBD} + \widehat {BCD}\,(3)\)
Trong ∆BCD, ta có:
\(\widehat {ADB} = \widehat {CBD} = \widehat {BCD}\) (tính chất góc ngoài) (4)
\(\widehat {ADB} = 45^\circ \) (vì ∆ABD vuông cân tại A) (5)
Từ (3), (4) và (5) suy ra: \(\widehat {AEB} + \widehat {BCD} = 45^\circ \)
* Cách 2:
Trong tam giác ABC, ta có:
\(tg\widehat {AEB} = {{AB} \over {AC}} = {a \over {2a}} = {1 \over 2}\)
Suy ra: \(\widehat {AEB} = 26^\circ 34’\)
Trong tam giác vuông ABC, ta có:
\(tg\widehat {ACB} = {{AB} \over {AC}} = {a \over {3a}} = {1 \over 3}\)
Suy ra: \(\widehat {ACB} = 18^\circ 26’\)
Vậy: \(\widehat {AEB} + \widehat {ACB} = \widehat {AEB} + \widehat {BCD} = 45^\circ \)
