Tam giác ABC có \(\hat A = 20^\circ ,\widehat B = 30^\circ ,AB = 60cm\). Đường vuông góc kẻ từ C đến AB cắt AB tại P. (h.33).
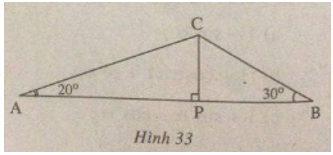
Hãy tìm:
a) AP, BP;
b) CP.
Gợi ý làm bài
a) Trong tam giác vuông ACP, ta có:
\(AP = CP.\cot g\widehat {PAC}\,(1)\)
Trong tam giác vuông BCP, ta có:
\(BP = CP.\cot g\widehat {PBC}\,(2)\)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra:
\((AP + BP) = CP.\cot g\widehat {PAC} + CP.\cot g\widehat {PBC}\)
Hay \(AB = CP(\cot g\widehat {PAC} + \cot g\widehat {PBC})\)
Suy ra:
\(\eqalign{
& CP = {{AB} \over {\cot g\widehat {PAC} + \cot g\widehat {PBC}}} \cr
& = {{AB} \over {\cot g20^\circ + \cot g30^\circ }} \approx 13,394\,(cm) \cr} \)
b) Thay CP = 13,394 vào (1) ta có:
\(AP = 13,394.\cot g20^\circ \approx 36,801\,(cm)\)
Thay CP = 13,394 vào (2) ta có:
\(BP = 13,394.\cot g30^\circ \approx 27,526\,(cm)\)
