Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng \(120^\circ \). Tính chu vi và diện tích của hình thang đó.
Gợi ý làm bài
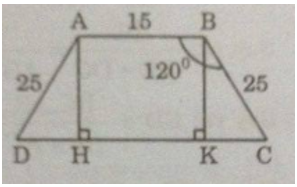
Giả sử hình thang ABCD có đáy nhỏ AB = 15cm, cạnh bên AD = BC =25cm, \(\widehat {ABC} = \widehat {BAD} = 120^\circ \).
Kẻ \(AH \bot CD,BK \bot CD\)
Vì ABKH là hình chữ nhật nên:
AB = KH =15 (cm)
Ta có:
\(\widehat {ADC} + \widehat {DAB} = 180^\circ \)
Suy ra:
\(\widehat {ADC} = 180^\circ - \widehat {DAB} = 180^\circ - 120^\circ = 60^\circ \)
Advertisements (Quảng cáo)
Trong tam giác vuông ADH, ta có:
\(\eqalign{
& DH = AD.\cos \widehat {ADC} \cr
& = 25.\cos 60^\circ = 12,5\,(cm) \cr} \)
\(\eqalign{
& AH = AD.\sin \widehat {ADC} \cr
& = 25.\sin 60^\circ = {{25\sqrt 3 } \over 2}\,)\,\,(cm) \cr} \)
Mà ∆ADH=∆BCK (cạnh huyền, cạnh góc vuông)
Suy ra: DH = CK = 12,5 (cm)
Chu vi hình thang ABCD là:
AB + BC + CD + DA = AB + BC + (CK + KH + HD) + DA
= 15 + 25 + (12,5 + 15 + 12,5) + 25 = 105 (cm)
Chu vi hình thang ABCD là:
\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr
& = {{15 + 40} \over 2}.{{25\sqrt 2 } \over 2} \approx 595,392\,\,\left( {c{m^2}} \right) \cr} \)
