Gọi AM, BN, CL là ba đường cao của tam giác ABC. Chứng minh:
a) ∆ANL đồng dạng ∆ABC;
b) AN.BL.CM = AB.BC.CA.cosA.cosB.cosC.
Gợi ý làm bài
a) Xét hai tam giác BNA và CLA, ta có:
\(\widehat {BNA} = \widehat {CLA} = 90^\circ \)
\(\widehat A\) chung
Suy ra ∆BNA đồng dạng ∆CLA (g.g)
Suy ra: \({{AL} \over {AN}} = {{AC} \over {AB}} \Rightarrow {{AL} \over {AC}} = {{AN} \over {AB}}\)
Xét hai tam giác ABC và ANL, ta có:
Advertisements (Quảng cáo)
\({{AL} \over {AC}} = {{AN} \over {AB}}\)
\(\widehat A\) chung
Suy ra ∆ABC đồng dạng ∆ANL (c.g.c
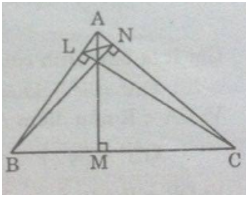
b) ABN vuông tại N nên \(AN = AB.\cos \widehat B\,(1)\)
∆BCL vuông tại L nên \(BL = BC.\cos \widehat B\,(2)\)
∆ACM vuông tại M nên \(CM = AC.\cos \widehat C\,(3)\)
Từ (1), (2) và (3) suy ra:
\(AN.BL.CM = AB.BC.CA.\cos \widehat A\cos \widehat B\cos \widehat C.\)
