Câu 9.1 trang 111 Sách Bài Tập (SBT) Toán 9 Tập 2
Tính chu vi của hình bên biết OA = OB = R > 0 (h.bs.5).
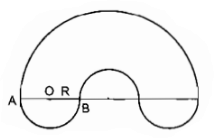
Giải
Hình đó gồm một nửa đường tròn bán kính 3R và 3 nửa đường tròn bán kính R
Chu vi của hình đó là:
\(l = {1 \over 2}.2\pi .3R + 3.{1 \over 2}.2\pi .R = 6\pi R\)
Câu 9.2 trang 111 Sách Bài Tập (SBT) Toán 9 Tập 2
Tính chu vi của hình cánh hoa, biết OA = R (h.bs.6).

Giải
Hình vẽ có 6 cung tròn bằng nhau có bán kính bằng R
Advertisements (Quảng cáo)
\(\overparen{BOF}\) của đường tròn (A; R)
\(\overparen{AOC}\) của đường tròn (B; R)
\(\overparen{BOD}\) của đường tròn (C; R)
\(\overparen{COE}\) của đường tròn (D; R)
\(\overparen{DOF}\) của đường tròn (E; R)
\(\overparen{EOA}\) của đường tròn (F; R)

∆AOB đều, ∆AOF đều nên \(\widehat {BAF} = {120^0}\)
\( \Rightarrow \) sđ \(\overparen{BOF}\)= 1200
\(l = {{\pi R.120} \over {180}} = {{2\pi R} \over 3}\)
Chu vi cánh hoa: \({{2\pi R} \over 3}.6 = 4\pi R\)
