Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a.
a) Tính \({{\sin B + c{\rm{osB}}} \over {\sin B - c{\rm{osB}}}}.\)
b) Tính chiều cao của hình thang ABCD.
Gợi ý làm bài
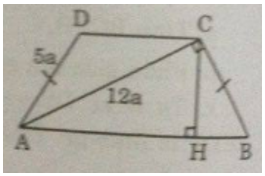
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(A{B^2} = B{C^2} + A{C^2} = {(5a)^2} + {(12a)^2} = 169{a^2}\)
Suy ra: \(AB = \sqrt {169{a^2}} = 13a\)
Advertisements (Quảng cáo)
Ta có: \(\sin \widehat B = {{AC} \over {AB}} = {{12a} \over {13a}} = {{12} \over {13}}\)
\(\cos \widehat B = {{BC} \over {AB}} = {{5a} \over {13a}} = {5 \over {13}}\)
Suy ra:
\({{\sin \widehat B + \cos \widehat B} \over {\sin \widehat B - \cos \widehat B}} = {{{{12} \over {13}} + {5 \over {13}}} \over {{{12} \over {13}} - {5 \over {13}}}} = {{{{17} \over {13}}} \over {{7 \over {13}}}} = {{17} \over {13}}.{{13} \over 7} = {{17} \over 7}\)
b) Kẻ \(CH \bot AB\)
Trong tam giác vuông BCH, ta có:
\(CH = CB.\sin \widehat B = 5a.{{12} \over {13}} = {{60a} \over {13}}\)
