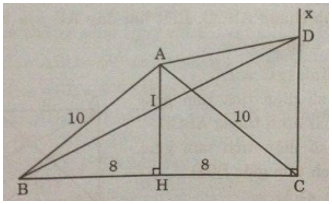
Cho tam giác cân ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho $AI = {1 \over 3}AH$. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D.
a) Tính các góc của tam giác ABC.
b) Tính diện tích tứ giác ABCD.
Gợi ý làm bài
Ta có: \(AH \bot BC\), suy ra: \(HB = HC = {{BC} \over 2} = 8\,(cm)\)
Trong tam giác vuông ABH, ta có:
\(\cos \widehat B = {{HB} \over {AB}} = {8 \over {10}} = 0,8\)
Suy ra: \(\widehat B \approx 36^\circ 52’\)
Vì ∆ABC cân nên \(\widehat B = \widehat C = 36^\circ 52’\)
Ta có:
\(\widehat A = 180^\circ - (\widehat B + \widehat C) = 180^\circ - (36^\circ 52′ + 36^\circ 52′) = 106^\circ 16’\)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& A{B^2} = A{H^2} + B{H^2} \cr
& \Rightarrow A{H^2} = A{B^2} - B{H^2} = {10^2} - {8^2} = 36 \cr} \)
Suy ra: AH = 6 (cm)
Ta có: \(AI = {1 \over 3}.AH = {1 \over 3}.6 = 2\,(cm)\)
Suy ra: IH = AH - AI = 6 - 2 = 4 (cm)
Vì \(IH \bot BC\) và $DC \bot BC$ nên IH // DC (1)
Mặt khác: BH = HC (gt) (2)
Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD
Suy ra: \(IH = {1 \over 2}CD\) hay CD = 2IH = 2.4 = 8 (cm)
Ta có:
\({S_{ABH}} = {1 \over 2}AH.BH = {1 \over 2}.6.8 = 24\,\,\left( {c{m^2}} \right)\)
\({S_{AHCD}} = {{AH + CD} \over 2}.HC = {{6 + 8} \over 2}.8 = 56\,\left( {c{m^2}} \right)\)
Vậy \({S_{ABCD}} = S{ _{ABH}} + {S_{AHCD}} = 24 + 56 = 80\,\) (cm2)
