Cho hình thang ABCD. Biết hai đáy AB = a và CD = 2a, cạnh bên AD = a, \(\widehat A = 90^\circ \)
a) Chứng minh \(tg\widehat C = 1.\)
b) Tính tỉ số diện tích tam giác BCD và diện tích hình thang ABCD.
c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD.
Gợi ý làm bài
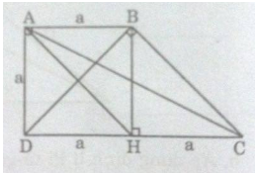
a) Kẻ \(BH \bot CD\)
Ta có: AB // CD và \(\widehat A = 90^\circ \)
Suy ra: \(\widehat D = 90^\circ \)
Tứ giác ABHD có ba góc vuông và AB = AD = a nên là hình vuông.
Advertisements (Quảng cáo)
Suy ra: DH = BH = AB = a
Ta có: CD = DH + HC
Suy ra: HC = CD – DH = 2a – a = a
Vậy \(tg\widehat C = {{BH} \over {CH}} = {a \over a} = 1\)
b) Ta có: \({S_{BCD}} = {1 \over 2}BH.CD = {1 \over 2}a.2a = {a^2}\) (đvdt)
\({S_{ABCD}} = {{AB + CD} \over 2}.AD = {{a + 2a} \over 2}.a = {3 \over 2}{a^2}\) (đvdt)
Vậy \({{{S_{BCD}}} \over {{S_{ABCD}}}} = {{{a^2}} \over {{3 \over 2}{a^2}}} = {1 \over {{3 \over 2}}} = {2 \over 3}.\)
c) Ta có: \({S_{ABC}} = {1 \over 2}a.a = {1 \over 2}{a^2}\) (đvdt)
Vậy \({{{S_{ABC}}} \over {{S_{BCD}}}} = {{{1 \over 2}{a^2}} \over {{a^2}}} = {1 \over 2}\)
