
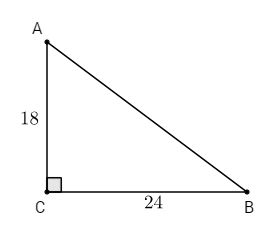
Cho tam giác ABC vuông tại C, cho biết AC = 18 cm và BC = 24 cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
Sử dụng định lý Pythagore, công thức tỷ số lượng giác và tỷ số lượng giác của hai góc phụ nhau.

Advertisements (Quảng cáo)
Áp dụng định lý Pythagore vào tam giác ABC vuông tại C:
\(A{B^2} = A{C^2} + B{C^2}\)
\(\Rightarrow AB = \sqrt {A{C^2} + B{C^2}} \)\(\, = \sqrt {{{18}^2} + {{24}^2}} = 30\) (cm)
\(\begin{array}{l} \Rightarrow \sin B = \dfrac{{AC}}{{AB}} = \dfrac{{18}}{{30}} = \dfrac{3}{5}\\\;\;\;\;\cos B = \dfrac{{BC}}{{AB}} = \dfrac{{24}}{{30}} = \dfrac{4}{5}\\\;\;\;\;\tan B = \dfrac{{AC}}{{BC}} = \dfrac{{18}}{{24}}\, = \dfrac{3}{4}\\\;\;\;\;\cot B = \dfrac{{BC}}{{AC}} = \dfrac{{24}}{{18}} = \dfrac{4}{3}\end{array}\)
Ta có tam giác ABC vuông tại C \(\widehat A + \widehat B = {90^o}\)
\(\begin{array}{l} \Rightarrow \sin A = \cos B = \dfrac{4}{5}\\\;\;\;\;\cos A = \sin B = \dfrac{3}{5}\\\,\,\,\,\,\,\;\tan A = \cot B = \dfrac{4}{3}\\ \,\,\,\,\;\;\cot A = \tan B = \dfrac{3}{4}\end{array}\)
