
Cho tam giác ABC vuông tại A có AB = 10 cm, AC = 15 cm.
a) Tính góc B.
b) Phân giác trong góc B cắt AC tại I. Tính AI.
c) Vẽ AH vuông góc với BI tại H. Tính AH.
a) Sử dụng tỉ số lượng giác tính góc B
b) Áp dụng định lý Pythagore và tính chất đường phân giác để có tổng và tỉ của IA,IC.
c) Áp dụng hệ thức lượng trong tam giác vuông.

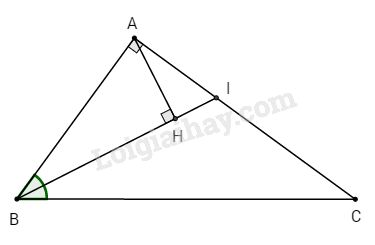
a) Tính góc B.
\(\tan {\widehat B} = \dfrac{{AC}}{{AB}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)
\(\Rightarrow {\widehat B} \approx {56^0}19’\)
Advertisements (Quảng cáo)
b) Phân giác trong góc B cắt AC tại I. Tính AI.
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A:
\(A{B^2} + A{C^2} = B{C^2} \)
\(\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} \)\(\,= \sqrt {{{10}^2} + {{15}^2}} = 5\sqrt {13} \)
AI là phân giác trong góc I nên ta có:
\(\dfrac{{IA}}{{IC}} = \dfrac{{BA}}{{BC}} = \dfrac{{10}}{{5\sqrt {13} }} = \dfrac{2}{{\sqrt {13} }} \)
\(\Rightarrow IC = \dfrac{{\sqrt {13} }}{2}IA\)
Mặt khác: \(IA + IC = AC = 15 \)
\(\Rightarrow IA + \dfrac{{\sqrt {13} }}{2}IA = 15 \)
\(\Rightarrow IA = \dfrac{{ - 20 + 10\sqrt {13} }}{3}\) cm
c) Vẽ AH vuông góc với BI tại H. Tính AH.
Áp dụng hệ thức lượng trong tam giác ABI vuông tại A, đường cao AH có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{I^2}}} \)\(\,= \dfrac{1}{{100}} + \dfrac{9}{{{{\left( { - 20 + 10\sqrt {13} } \right)}^2}}} \)
\(\Rightarrow A{H^2} \approx 22,26 \Rightarrow AH \approx 4,72\)cm
