
Tính diện tích đường tròn ngoại tiếp và hình tròn nội tiếp một hình vuông có cạnh 10 cm.
Sử dụng công thức tính diện tích hình tròn bán kính R là \(S = \pi {R^2}\).

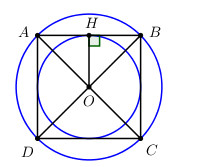
Gọi \(O = AC \cap BD\). Gọi H là trung điểm của AB ta có \(OH \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).
Advertisements (Quảng cáo)
Bán kính đường tròn ngoại tiếp hình vuông ABCD là OA.
Áp dụng định lí Pytago trong tam giác vuông OAB có : \(O{A^2} + O{B^2} = A{B^2}\)
\( \Rightarrow 2O{A^2} = {10^2} = 100 \Leftrightarrow O{A^2} = 50 \Leftrightarrow OA = 5\sqrt 2 \).
\( \Rightarrow \) Diện tích hình tròn ngoại tiếp hình vuông ABCD là \(S = \pi O{A^2} = \pi .{\left( {5\sqrt 2 } \right)^2} = 50\pi \approx 157\,\,\left( {c{m^2}} \right)\).
Bán kính đường tròn nội tiếp hình vuông ABCD là OH.
Ta có \(OH = \dfrac{1}{2}AB = 5\,\,\left( {cm} \right)\)(Định lí đường trung tuyến trong tam giác vuông)
\( \Rightarrow \) Diện tích hình tròn nội tiếp hình vuông ABCD là \(S’ = \pi O{H^2} = 25\pi \approx 78,5\,\,\left( {c{m^2}} \right)\)
