
Từ điểm A trên nửa đường tròn (O) đường kính BC, vẽ ra ngài tam giác ABC hai nửa đường tròn đường kính AB và AC (AB<AC, xem hình vẽ). Chứng minh rằng: diện tích S của tam giác ABC bằng tổng hai diện tích S1 và S2 của hai hình trăng khuyết là phần của hai nửa đường tròn đường kính AB và AC ở ngoài nửa đường tròn đường kính BC.
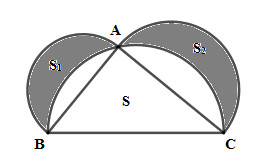
Sử dụng công thức tính diện tích hình tròn và định lí Pytago.

Advertisements (Quảng cáo)
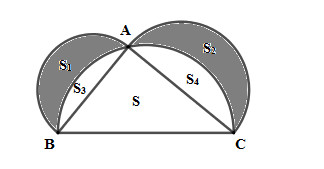
Diện tích nửa hình tròn đường kính AB là \(\pi {\left( {\dfrac{{AB}}{2}} \right)^2} = {S_1} + {S_3} \Rightarrow {S_1} = \pi {\left( {\dfrac{{AB}}{2}} \right)^2} - {S_3}\)
Diện tích nửa hình tròn đường kính AC là \(\pi {\left( {\dfrac{{AC}}{2}} \right)^2} = {S_2} + {S_4} \Rightarrow {S_3} = \pi {\left( {\dfrac{{AC}}{2}} \right)^2} - {S_4}\)
\(\begin{array}{l} \Rightarrow {S_1} + {S_2} = \pi {\left( {\dfrac{{AB}}{2}} \right)^2} - {S_3} + \pi {\left( {\dfrac{{AC}}{2}} \right)^2} - {S_4} = \pi {\left( {\dfrac{{AB}}{2}} \right)^2} + \pi {\left( {\dfrac{{AC}}{2}} \right)^2} - \left( {{S_3} + {S_4}} \right)\\ \Rightarrow {S_1} + {S_2} = \dfrac{\pi }{4}\left( {A{B^2} + A{C^2}} \right) - \left( {{S_3} + {S_4}} \right)\end{array}\)
Diện tích nửa hình tròn đường kính BC là \(\pi {\left( {\dfrac{{BC}}{2}} \right)^2} = {S_3} + {S_4} + S \Rightarrow S = \pi {\left( {\dfrac{{BC}}{2}} \right)^2} - \left( {{S_3} + {S_4}} \right)\)
Vì \(\widehat {BAC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ABC\) vuông tại A.
Áp dụng định lí Pytago ta có: \(B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow {S_1} + {S_2} = \dfrac{\pi }{4}.B{C^2} - \left( {{S_3} + {S_4}} \right) = \dfrac{\pi }{4}{\left( {\dfrac{{BC}}{2}} \right)^2} - \left( {{S_3} + {S_4}} \right) = S\).
Vậy \(S = {S_1} + {S_2}\).
