
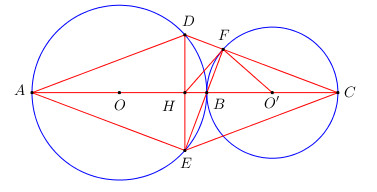
Trên đườn thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.
a) Chứng minh rằng đường tròn (O) và (O’) tiếp xúc ngoài tại B.
b) Vẽ dây DE vuông góc với AC tại H là trung điểm của AC. Chứng minh tứ giác ADCE là hình thoi.
c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.
d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).
a) Chứng minh \(OB + O’B = OO’\).
b) Chứng minh tứ giác \(ADCE\) có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.
c) Chứng minh BE và BF cùng vuông góc với AE.
d) Chứng minh \(HF \bot O’F\).

a) Ta có \(OB + O’B = OO’ \Rightarrow \left( O \right)\)và \(\left( {O’} \right)\) tiếp xúc ngoại tại \(B\) .
b) Vì \(AC \bot DE\) tại \(H \Rightarrow H\) là trung điểm của \(DE\) (quan hệ vuông góc giữa đường kính và dây cung),
Xét tứ giác \(ADCE\) có hai đường chéo \(AC\) và \(DE\) cắt nhau tại trung điểm mỗi đườn g\( \Rightarrow ADCE\) là hình bình hành. Lại có \(AC \bot DE \Rightarrow ADCE\) là hình thoi (Hình bình hành có hai đường chéo vuông góc).
Advertisements (Quảng cáo)
c) Do \(E\) thuộc đường tròn đường kính \(AB \Rightarrow \angle AEB = {90^0} \Rightarrow BE \bot AE\).
Do \(F\) thuộc đường tròn đường kính \(BC \Rightarrow \angle BFC = {90^0} \Rightarrow BF \bot CD\).
Vì \(ADCE\) là hình thoi (cmt) \( \Rightarrow AE//CD \Rightarrow BF \bot AE\).
Qua điểm B không thuộc \(AE\) ta có \(\left\{ \begin{array}{l}BE \bot AE\\BF \bot AE\end{array} \right. \Rightarrow B,E,F\)thẳng hàng.
d) Xét tam giác vuông BCF có \(\angle BCF + \angle CBF = {90^0}\)
Xét tam giác vuông CDH có : \(\angle CBF + \angle CDH = {90^0}\)
\( \Rightarrow \angle CBF = \angle CDH\).
Ta có \(O’B = O’F \Rightarrow \Delta O’BF\) cân tại \(O’ \Rightarrow \angle O’BF = \angle O’FB\) \( \Rightarrow \angle CBF = \angle O’FB\).
\( \Rightarrow \angle O’FB = \angle CDH\) .
Xét tam giác vuông DEF có \(HE = \dfrac{1}{2}DE = HD = HE \) \(\Rightarrow \Delta HED\) cân tại \(H\).
\( \Rightarrow \angle HDF = \angle HFD \)
\(\Rightarrow \angle CDH = \angle HFD \)
\(\Rightarrow \angle O’FB = \angle HFD\).
Mà \(\angle HFD + \angle HFB = {90^0} \) \(\Rightarrow \angle O’EB + \angle HFB = {90^0} \) \(\Leftrightarrow \angle O’FH = {90^0}\)
\( \Rightarrow HF \bot O’F\). Mà \(O’F\) là bán kính của \(\left( {O’} \right)\).
Vậy \(HF\) là tiếp tuyến của \(\left( {O’} \right)\).
Baitapsgk.com
