
Cho nửa đường tròn (O) có đường kính AB = 2R. Vẽ bán kính OC vuông góc với AB, gọi M là một điểm nằm trên OC sao cho \(\tan \widehat {OAM} = \dfrac{3}{4}\), AM cắt nửa đường tròn tại D. Tính các đoạn AM, AD, BD theo R.
Sử dụng các tỉ số lượng giác, tỉ lệ đồng dạng và định lý Pythagore để tính.

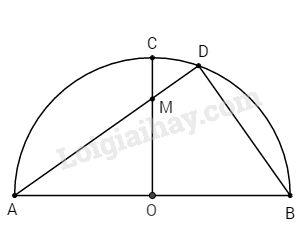
Xét tam gác OAM vuông tại O có:
\(\tan \widehat {OAM} = \dfrac{{OM}}{{OA}} = \dfrac{3}{4} \)
\(\Rightarrow OM = \dfrac{3}{4}OA = \dfrac{3}{4}R\)
Advertisements (Quảng cáo)
Áp dụng định lý Pythagore vào tam giác OAM vuông tại O:
\(A{M^2} = O{A^2} + O{M^2}\)
\(\Rightarrow AM = \sqrt {O{A^2} + O{M^2}} \)\(\, = \sqrt {{R^2} + \dfrac{9}{{16}}{R^2}} = \dfrac{5}{4}R\)
D là một điểm trên nửa đường tròn (O) \( \Rightarrow \widehat {ADB} = {90^o}\) (góc nội tiếp chắn nửa đường tròn)
Xét hai tam giác OAM và DAB có:
+) \(\widehat A\) chung;
+) \(\widehat {AOM} = \widehat {ADB} = {90^o}\)
\( \Rightarrow \)Hai tam giác OAM và DAB đồng dạng
\(\begin{array}{l} \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{{OA}}{{AD}} = \dfrac{{OM}}{{BD}}\\ \Rightarrow AD = \dfrac{{OA.AB}}{{AM}} = \dfrac{{R.2R}}{{\dfrac{5}{4}R}} = \dfrac{8}{5}R\\ BD = \dfrac{{OM.AB}}{{AM}} = \dfrac{{\dfrac{3}{4}R.2R}}{{\dfrac{5}{4}R}} = \dfrac{6}{5}R\end{array}\)
