
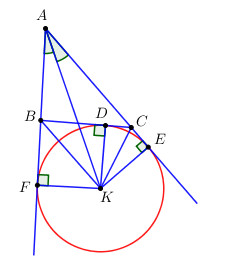
Gọi K là giao điểm đường phân giác của góc A với các đường phân giác của hai góc ngoài tại B và C của tam giác ABC. D, E, F lần lượt là chân đường vuông góc hạ từ K xuống các đường thẳng BC, AC, AB.
a) Chứng minh rằng KD = KF.
b) Chứng minh rằng KD = KE. Suy ra ba điểm D, E và F cùng nằm trên một đường tròn.

Advertisements (Quảng cáo)
a) Xét hai tam giác vuông \({\Delta _v}BKF\) và \({\Delta _v}BKD\) có:
\(\begin{array}{l}BK\,\,chung\\\widehat {KBF} = \widehat {KBD}\,\,\left( {gt} \right)\end{array}\)
\( \Rightarrow {\Delta _v}BKF = {\Delta _v}BKD\) (cạnh huyền – góc nhọn) \( \Rightarrow KD = KF\) (2 cạnh tương ứng)
b) Hoàn toàn tương tự ta chứng minh được \(\Delta CKD = \Delta CKE\) (cạnh huyền – góc nhọn) \( \Rightarrow KD = KE\) (2 cạnh tương ứng).
Vậy \(KD = KE = KF\) hay các điểm \(D,\,\,E,\,\,F\) cùng thuộc một đường tròn \(\left( {K;KD} \right)\).
Baitapsgk.com
