Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng. Bài 10 trang 104 sgk Toán 9 - tập 1 - Bài 2. Đường kính và dây của đường tròn
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC
Hướng dẫn giải:
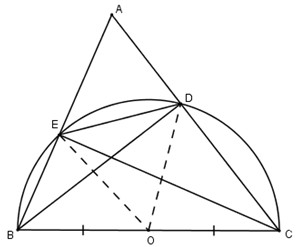
a) Gọi O là trung điểm của BC.
Advertisements (Quảng cáo)
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
\(EO=\frac{1}{2}BC; DO=\frac{1}{2}BC.\)
Suy ra \(OE=OD=OB=OC(=\frac{1}{2}BC)\)
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường \(\left( {O;{{BC} \over 2}} \right)\), BC là đường kính, DE là một dây không qua tâm, do đó DE<BC.
