Một mặt phẳng chứa trụ OO' của một hình trụ; phần mặt phẳng nằm trong hình trụ là một hình chữ nhật có chiều dài 3cm, chiều rộng 2cm.Tính diện tích xung quanh và thể tích hình trụ đó.. Bài 16 trang 135 SGK Toán 9 tập 2 - Phần Hình học - Ôn tập cuối năm - Toán 9
Bài 16. Một mặt phẳng chứa trụ \(OO’\) của một hình trụ; phần mặt phẳng nằm trong hình trụ là một hình chữ nhật có chiều dài \(3cm\), chiều rộng \(2cm\).Tính diện tích xung quanh và thể tích hình trụ đó.
Hướng dẫn làm bài:
Bài toán có 2 trường hợp
a) Đường cao của hình trụ bằng \(3cm\). Khi đó chiều rộng của hình chữ nhật là đường kính của hình trụ, suy ra \(R = 1cm\)
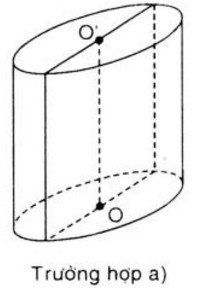
Vậy \(S\)xq = \(2πRh = 2π .1 .3 = 6π\) (\(cm^2\))
Advertisements (Quảng cáo)
\(V = πR^2h = π. 1^2. 3 = 3π\) (\(cm^3\))
b) Đường cao hình trụ bằng \(2cm\)
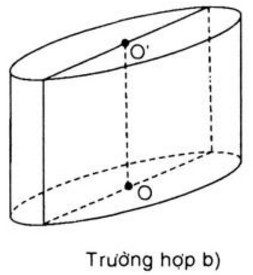
khi đó chiều dài của hình chữ nhật là đường kính của hình trụ, suy ra \(R = 1,5\)
Vậy \(S\)xq = \(2πRh = 2π . 1,5 . 2 = 6π\) (\(cm^2\))
\(V = πR^2h = π . 1,5^2 . 2 = 4,5 π\) (\(cm^2\))