Bài 15. Tam giác \(ABC\) cân tại \(A\) có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn \((O)\).Tiếp tuyến tại \(B\) và \(C\) của đường tròn lần lượt cắt tia \(AC\) và tia \(AB\) ở \(D\) và \(E\). Chứng minh:
a) \(BD^2 = AD.CD\)
b) Tứ giác \(BCDE\) là tứ giác nội tiếp
c) \(BC\) song song với \(DE\)
Hướng dẫn làm bài:
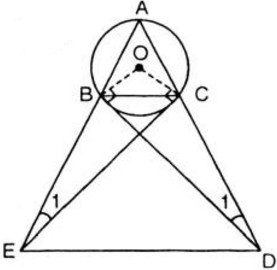
a) Xét \(∆ADB\) và \(∆BDC\), ta có:
\(\widehat {BA{\rm{D}}} = \widehat {CB{\rm{D}}}\) (góc nội tiếp cùng chắn cung \(BC\))
\(\widehat {{D_1}}\) góc chung
Vậy \(∆ADB\) đồng dạng \(∆BDC\) ⇒ \({{B{\rm{D}}} \over {C{\rm{D}}}} = {{A{\rm{D}}} \over {B{\rm{D}}}} = B{{\rm{D}}^2} = A{\rm{D}}.C{\rm{D}}\) (đpcm)
Advertisements (Quảng cáo)
b) Ta có \(\widehat {A{\rm{E}}C}\) là góc có đỉnh ở bên ngoài \((O)\)
\(\widehat {AEC} = {sđ\overparen{AC}-sđ\overparen{BC}\over 2} = { sđ\overparen{AB}-sđ\overparen{BC}\over 2} = \widehat {ADB}\)
Xét tứ giác \(BCDE\), ta có: \(\widehat {A{\rm{E}}C}\) và \(\widehat {ADB}\) là hai góc liên tiếp cùng nhìn đoạn \(BC\) và \(\widehat {A{\rm{E}}C} = \widehat {ADB}\) . Vậy tứ giác \(BCDE\) nội tiếp đường tròn
c) Ta có: \(\widehat {ACB} + \widehat {BC{\rm{D}}} = {180^0}\) (hai góc kề bù).
hay \(\widehat {ABC} + \widehat {BC{\rm{D}}} = {180^0}\) (\(∆ABC\) cân tại \(A\))
\( \Rightarrow \widehat {ABC} = {180^0} - \widehat {BC{\rm{D}}}(1)\)
Vì \(BCDE\) là tứ giác nội tiếp nên
\(\widehat {BE{\rm{D}}} + \widehat {BC{\rm{D}}} = {180^0} \Rightarrow \widehat {BE{\rm{D}}} = {180^0} - \widehat {BC{\rm{D}}}(2)\)
So sánh (1) và (2), ta có: \(\widehat {ABC} = \widehat {BE{\rm{D}}}\)
Ta cũng có: \(\widehat {ABC}\) và \(\widehat {BE{\rm{D}}}\) là hai góc đồng vị. Suy ra: \(BC // DE\) (đpcm)
