Bài 23 Viết công thức tính nửa góc ở đỉnh của một hình nón (góc a của tam giác vuông AOS- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính SA).. Bài 23 trang 119 - Sách giáo khoa toán 9 tập 2 - Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón hình nón cụt
Bài 23 Viết công thức tính nửa góc ở đỉnh của một hình nón (góc \(a\) của tam giác vuông \(AOS\)- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính \(SA\)).
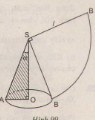
Giải:
Diện tích hình quạt :
\(S_q = \frac{\pi r^2 n^o}{360^o}= \frac{\pi.l^2.90}{360}=\frac{\pi.l^2}4\)
Advertisements (Quảng cáo)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\)
Theo đầu bài ta có: \({S_{xq}} = S_q \)=> \(πrl\)= \(\frac{\pi.l^2}4\)
Vậy \(l = 4r\)
Suy ra \(sin(a) \)= \(\frac{r}l\) =\( 0,25\)
Vậy \(a = {14^0}28’\)
