Bài 23. Cho đường tròn \((O)\) và một điểm \(M\) cố định không nằm trên đường tròn. Qua \(M\) kẻ hai đường thẳng. Đường thẳng thứ nhất cắt \((O)\) tại \(A\) và \(B\).Đường thẳng thứ nhất cắt \((O)\) tại \(C\) và \(D\).
Chứng minh \(MA. MB = MC. MD\)
Hướng dẫn giải:
Xét hai trường hợp:
a) \(M\) ở bên trong đường tròn (hình a)
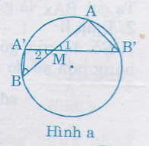
Xét hai tam giác \(MAB’\) và \(MA’B\) có:
\(\widehat{M_{1}}\) = \(\widehat{M_{2}}\) ( đối đỉnh)
\(\widehat{B’}\) = \(\widehat{B}\) (hai góc nội tiếp cùng chắn cung \(AA’\)).
Do đó \(∆MAB’\) đồng dạng \(∆MA’B\), suy ra:
Advertisements (Quảng cáo)
\(\frac{MA}{MA’}\) = \(\frac{MB’}{MB}\), do đó \(MA. MB = MB’. MA’\)
b) \(M ở bên ngoài đường tròn (hình b)
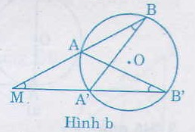
Tương tự ta có:
\(∆MAB’\) đồng dạng \(∆MA’B\)
\(\widehat{M}\) chung
\(\widehat{B’}\) = \(\widehat{B}\) (hai góc nội tiếp cùng chắn cung \(AA’\)).
Suy ra: \(\frac{MA}{MA’}\) = \(\frac{MB’}{MB}\)
hay \(MA. MB = MB’. MA’\)
